APLICACIONES DE LOS NÚMEROS COMPLEJOS

Aplicaciones a la Trigonometría

Partiendo de la formula de Euler podemos derivar una gran cantidad de identidades

De la trigonometría. Veamos entonces como el seno y el coseno se definen a

Partir de la funcion exponencial.

Tenemos la formula de Euler    eiθ = cos θ + isen θy luego e−iθ =cos(−θ) + isen(−θ) = cos θ − isen θ

Combinando las expresiones obtenemos las conocidas formulas que relacionan

seno y coseno con la exponencial

cos θ =eiθ + e−iθ2(3.10)y

sen θ =eiθ − e-iθ 2i(3.11)

Como una primera muestra del poder de los numero ´ s complejos en el estudio de

la trigonometría, derivamos las identidades para sen(θ + α) y cos(θ + α). Esto es

cos(θ + α) + isen(θ + α) = ei(θ+α) = e

iθ e iα= (cos θ + isen θ)(cos α + isen α) = (cos θ cos α − sen θ sen α) + i(sen θ cos α + cos θ sen α)

Igualando componentes en ambos lados nos quedan el par de formulas

cos(θ + α) = cos θ cos α − sen θ sen α

sen(θ + α) = sen θ cos α + cos θ sen α

En matemáticas 

Soluciones de ecuaciones polinómicas

Un raíz o cero2 del polinomio p es un complejo z tal que p(z)=0;

Un resultado importante de esta definición es que todas las ecuaciones polinómicas (algebraicas) de grado n tienen exactamente n soluciones en el cuerpo de los números complejos, esto es, tiene exactamente n complejos z que cumplen la igualdad p(z)=0, contados con sus respectivas multiplicidades. También se cumple que si z es una raíz entonces su conjugado también es una raíz del polinomio p. A esto se lo conoce como Teorema Fundamental del Álgebra, y demuestra que los complejos son un cuerpo algebraicamente cerrado; por esto los matemáticos consideran a los números complejos unos números más naturales.  Que los números reales a la hora de resolver ecuaciones

Variable compleja o análisis complejO

Artículo principal: Análisis complejo

Al estudio de las funciones de variable compleja se lo conoce como el Análisis complejo. Tiene una gran cantidad de usos como herramienta de matemáticas aplicadas así como en otras ramas de las matemáticas. El análisis complejo provee algunas importantes herramientas para la demostración de teoremas incluso en teoría de números; mientras que las funciones reales de variable real, necesitan de un plano cartesiano para ser representadas; las funciones de variable compleja necesitan un espacio de cuatro dimensiones, lo que las hace especialmente difíciles de representar. Se suelen utilizar ilustraciones coloreadas en un espacio de tres dimensiones para sugerir la cuarta coordenada o animaciones en 3D para representar las cuatro.

Ecuaciones diferenciales

En ecuaciones diferenciales, cuando se estudian las soluciones de las ecuaciones diferenciales lineales con coeficientes constantes, es habitual encontrar primero las raíces (en general complejas) \lambda\, del polinomio característico, lo que permite expresar la solución general del sistema en términos de funciones de base de la forma: f(x) = e^{\lambda x} \,.

Fractales

Artículo principal: Fractal

Muchos objetos fractales, como el conjunto de Mandelbrot, pueden obtenerse a partir de propiedades de convergencia de una sucesión de números complejos. El análisis del dominio de convergencia revela que dichos conjuntos pueden tener una enorme complejidad autosimilar.

En física

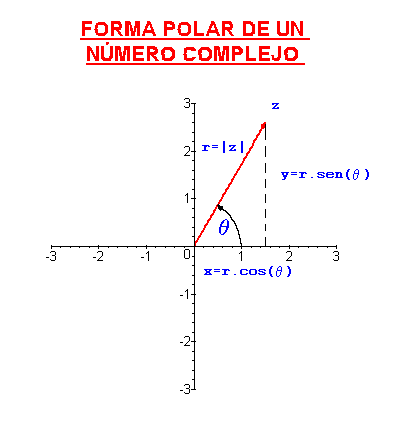
Los números complejos se usan en ingeniería electrónica y en otros campos para una descripción adecuada de las señales periódicas variables (ver Análisis de Fourier). En una expresión del tipo z=r e^{i \phi} \, podemos pensar en r\, como la amplitud y en  \phi \, como la fase de una onda sinusoidal de una frecuencia dada. Cuando representamos una corriente o un voltaje de corriente alterna (y por tanto con comportamiento sinusoidal) como la parte real de una función de variable compleja de la forma f(t)=z e^{i \omega t} \, donde ω representa la frecuencia angular y el número complejo z nos da la fase y la amplitud, el tratamiento de todas las fórmulas que rigen las resistencias, capacidades e inductores pueden ser unificadas introduciendo resistencias imaginarias para las dos últimas (ver redes eléctricas). Ingenieros eléctricos y físicos usan la letra j para la unidad imaginaria en vez de i que está típicamente destinada a la intensidad de corriente.

El campo complejo es igualmente importante en mecánica cuántica cuya matemática subyacente utiliza Espacios de Hilbert de dimensión infinita sobre C (ℂ).

En la relatividad especial y la relatividad general, algunas fórmulas para la métrica del espacio-tiempo son mucho más simples si tomamos el tiempo como una variable imaginaria.

Transcripción de Números Complejos en la vida diaria.Números Complejos

En la vida diaria.

• Aerodinámica
• En líneas de corrientes Circuitos Eléctricos

• En todo aparato eléctricoPor ejemplo, amplificadores, filtros, motores, generadores de energía eléctrica, líneas de transmisión de energía eléctrica.
• Señales Electrónicas
• Se emplea en formatos de compresión, transmisión en banda ancha, amplificadores de señales, procesamiento digital de señales, transmisión eléctrica, centrales hidroeléctricas.
• Lo aplicamos en varios aspectos comoOperaciones con Complejos ,para desarrollar las operaciones adecuadamente desde el colegio y así desarrollarlo y mejorar los a lo que sigue de nuestra vida profesional.