1. Forma binómica
Podemos considerar C como un espacio vectorial isomorfo a 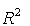 , de este modo se tiene:
, de este modo se tiene:
Gráficamente, podemos representar 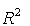 (y por tanto C) como un plano.
(y por tanto C) como un plano.
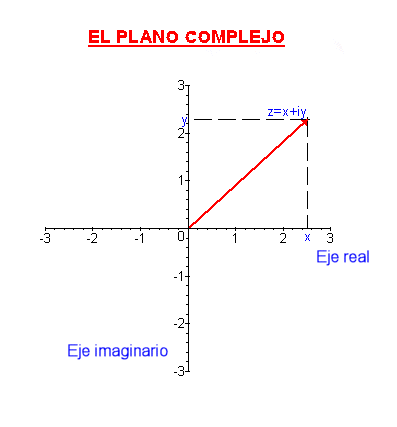
Para cada número complejo z, la primera componente, x, se denomina parte real y la segunda, y, se denomina parte imaginaria.
Obviamente, dos números complejos son iguales si y sólo si lo son simultáneamente sus partes reales y sus partes imaginarias.
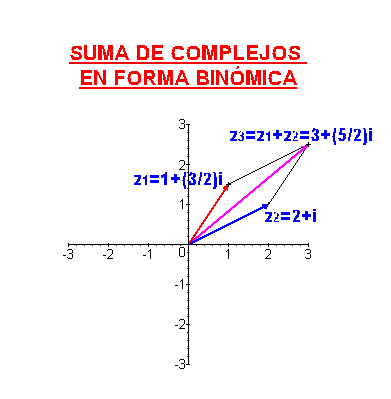
Usando este tipo de representación, la suma de complejos se corresponde con la suma de vectores. Dados dos vectores 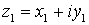 y
y 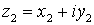 su suma es
su suma es 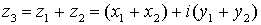
Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si 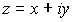 , entonces el módulo de
, entonces el módulo de  es
es 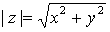 .
.
El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si 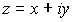 , entonces el conjugado de
, entonces el conjugado de  es
es 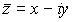 .
.
El opuesto de un número complejo es su simétrico respecto del origen.
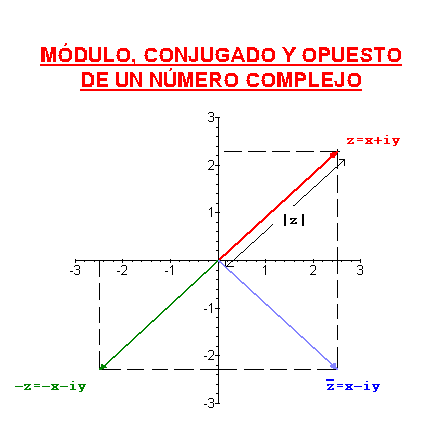
Es fácil ver que se cumple, 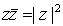 , por tanto podemos expresar el inverso de un número
, por tanto podemos expresar el inverso de un número 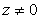 en la forma
en la forma 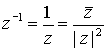 .
.
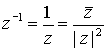 .
.
En vez de usar coordenadas cartesianas para representar a los puntos del plano podemos usar coordenadas polares, lo que da lugar a la siguiente forma de representación de los números complejos.
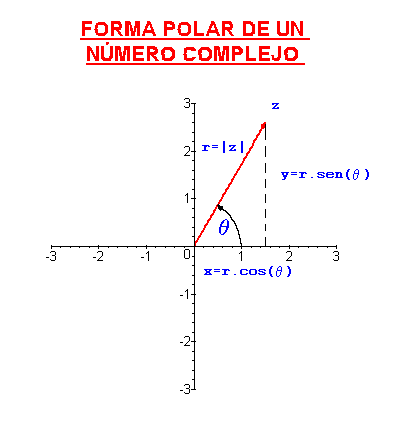
2. Forma polar o módulo-argumento
Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento,
donde 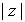 es el módulo de
es el módulo de  , y donde q es un argumento de
, y donde q es un argumento de  , esto es, q es un ángulo tal que
, esto es, q es un ángulo tal que
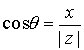 ,
, 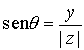 .
.
NOTA: Un número complejo tiene infinitos argumentos distintos. De hecho se puede definir el argumento de un número complejo no nulo como el conjunto de todos los posibles valores q que verifican lo anterior, es decir,
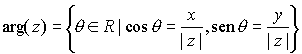
Es claro, por tanto, que si 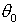 es un valor particular del argumento de
es un valor particular del argumento de  , entonces
, entonces
Se denomina argumento principal al único valor 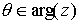 tal que
tal que 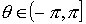 , y se denota
, y se denota 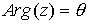
Se verifica entonces que
Dos números complejos 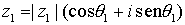 y
y 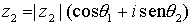 , representados en forma polar son iguales si y sólo si sus módulos son iguales
, representados en forma polar son iguales si y sólo si sus módulos son iguales 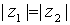 , y sus argumentos se diferencian en un número entero de vueltas, es decir,
, y sus argumentos se diferencian en un número entero de vueltas, es decir, 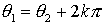 , con
, con 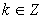 .
.
La forma polar de un número complejo es especialmente cómoda a la hora de multiplicar, ya que basta con multiplicar los módulos y sumar los argumentos, es decir, si 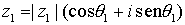 , y
, y 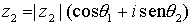 , entonces
, entonces
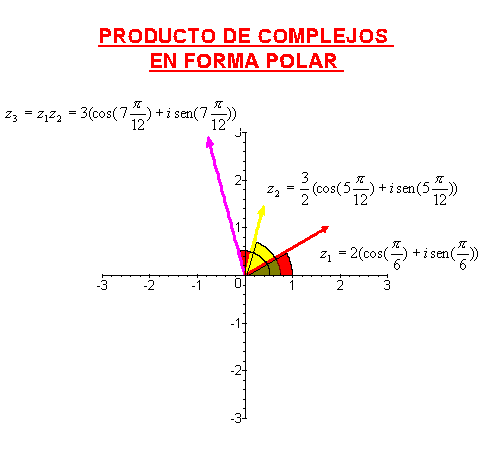
Del mismo modo se puede calcular el cociente de un complejo por otro no nulo sin más que dividir los módulos y restar los argumentos:
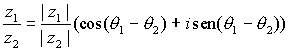 ,
,
siempre que 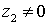 .
.
Las fórmulas anteriores pueden generalizarse para el producto de varios complejos, así, si 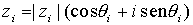 , para
, para 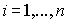 , entonces
, entonces
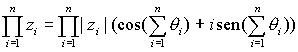
Finalmente, en el caso en que todos los factores sean iguales se obtiene la fórmula de Moivre:
Esta fórmula es también válida para exponentes enteros negativos, siempre que 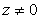 .
.
En particular tenemos otra expresión para el inverso de un número no nulo, 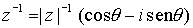 .
.
3. Forma exponencial
Una variante de la forma polar se obtiene al tener en cuenta la conocida como fórmula de Euler:
para 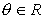 .
.
Esto nos permite escribir un número complejo en la forma siguiente, denominada forma exponencial:
Esta nueva forma es especialmente cómoda para expresar productos y cocientes ya que sólo hay que tener en cuenta las propiedades de la función exponencial (para multiplicar se suman exponentes y para dividir se restan). En particular, para potencias con exponentes enteros se tiene 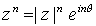 .
.
Esto nos permite dar una nueva expresión para el inverso de un complejo no nulo en la forma 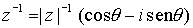 .
.




Harrah's Reno Resort & Casino - The JT Hub
ResponderEliminarExplore a 안양 출장마사지 world of luxury at Harrah's Reno 광양 출장마사지 Resort & Casino 강릉 출장샵 and enjoy 하남 출장안마 an unparalleled travel 대구광역 출장안마 experience at Harrah's Reno. Book the hotel with JT