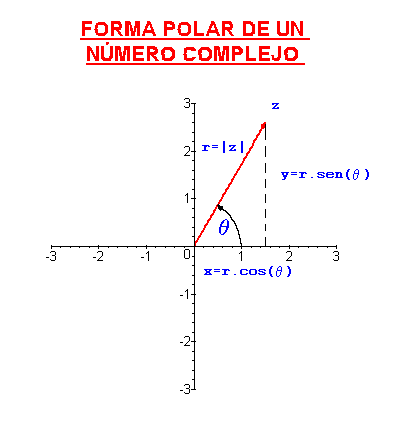
Estudiemos ahora las potencias con exponente racional de un número complejo. Dado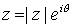 
, sea 
, para un número natural p.
, sea 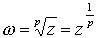, para un número natural p.
Si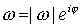 
, puesto que 
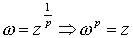, es decir, 
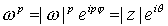. Por tanto, 
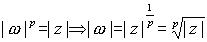, y además, 
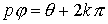, o sea, 
, para 
.
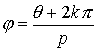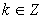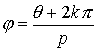, puesto que , es decir, . Por tanto, , y además, , o sea, , para .
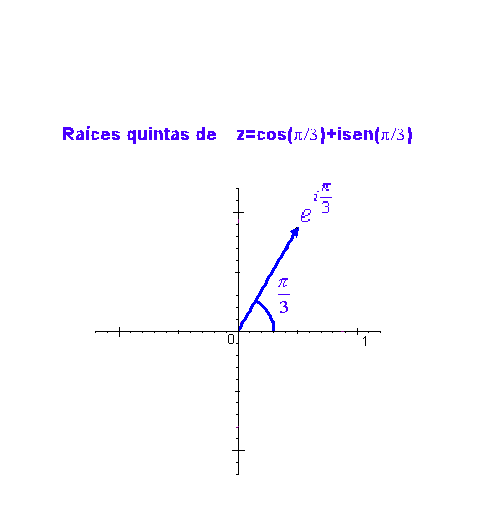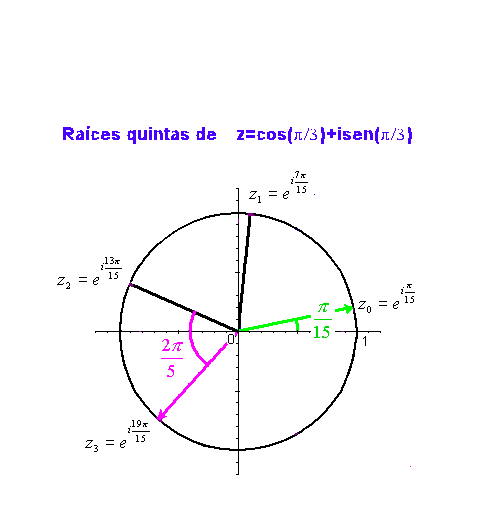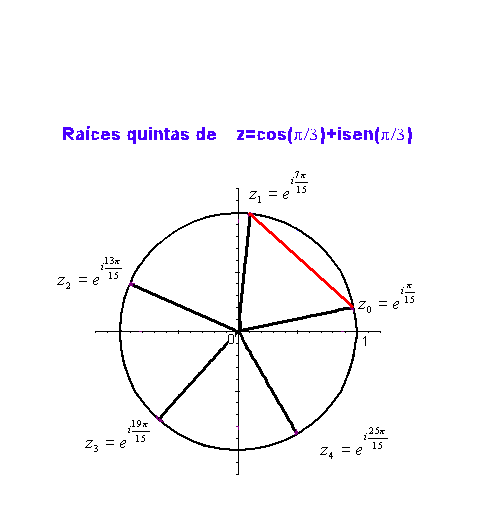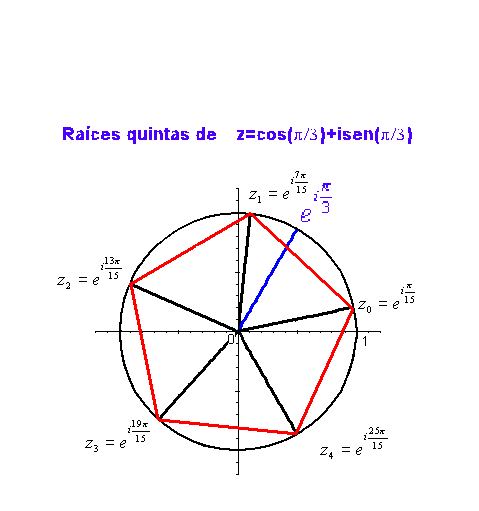
De todos estos valores sólo p consecutivos son distintos, el resto resulta ser repetición sucesiva de valores ya obtenidos. Por tanto, un número complejo tiene siempre p raíces p-ésimas distintas
, para 
.
Se puede observar que las p raíces pésimas tienen todas el mismo módulo, y sus argumentos se diferencian en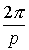 
cada uno del siguiente, esto es, las raíces p-ésimas se encuentran en los vértices de un polígono regular de p lados incrito en la circunferencia de centro 0 y radio 
.
cada uno del siguiente, esto es, las raíces p-ésimas se encuentran en los vértices de un polígono regular de p lados incrito en la circunferencia de centro 0 y radio .
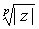Como ejemplo, en la siguiente gráfica podemos ver las raíces quintas de 
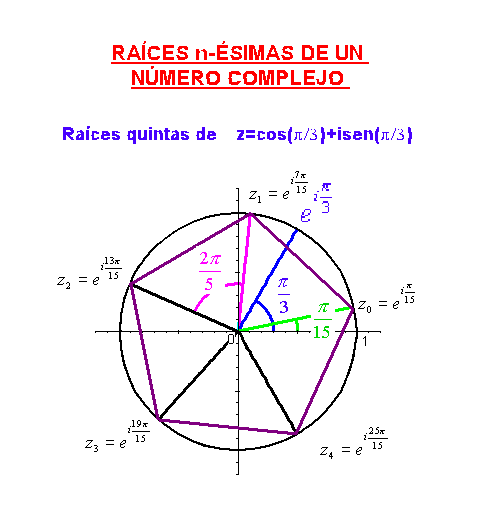
Puede verse lo mismo en la siguiente animación:
No hay comentarios:
Publicar un comentario